الحركية الإنزيمية لمادة تفاعل واحدة Cinétique enzymatique à un seul substrat

 

نموذج الحركة ل Michaélisيسمح بدراسة الخواص الحركية للإنزيمات˛ و تتم الدراسة في المرحلة الثابتة للتفاعل الإنزيميPhase stationnaire de la réaction enzymatique. للبرهان علي معادلة السرعة نتبع الخطوات التالية:

                                                             K+1                         k+2

    E+S                         ES                      E+P     (1)

                                                               k -1                             k-2

k+1 = constante de vitesse de la  réaction aller  E + S  (ثابت السرعة للتفاعل الأمامي)

 k-1 = constante de vitesse de la réaction ES (ثابت السرعة للتفاعل العكسي)

 k+2 = constante de vitesse de la réaction de ES en E + P.

k- 2= constante de vitesse de la réaction de E + P en ES .

تتم دراسة الحركية الإنزيمية في بداية التفاعل ( بداية المرحلة الثابتة) و عندها يكون تركيز مهمل و الخطوة العكسية غير مؤثرة علي الحركية و منه يمكن كتابة المعادلة كما يلي:

                                              K+1                                K+2                                                   

E + S                     ES                                  E    +     P  (2)

K-1                                                                                                

        

يمكن قياس النشاط الانزيمي من خلال تتبع سرعة التفاعل˛ ويمكن حساب السرعة من خلال العلاقة التالية: 

       (3)      vi =+ d(P) /d(t) ou –d(S)/ d(t)

 و بما أن تشكل الناتج أو اختفاء مادة التفاعل يتناسب مع تفكك و تشكيل المعقد الوسطي حسب الحالة فانه يمكن كتابة:

vi = K+2 (ES)    4

 

  يتكون (ES)  في كل لحظة زمنية وفقا لمعدلة من الدرجة الثانية:

E  +  S                         ES         (5)                             

               و يختفي في كل لحظة و فقا لمعادلتين من الدرجة الأولي:

ES    E + S et ES     E + P                                                                           و منه                  (6)        + d(ES) / d(t)  =   K+1 (E) (S)                          

-d(ES) /d(t) = k-1 (ES) +K+2 (ES)  (7)

بما أن الدراسة تتم في المرحلة الثابتة و التي تتميز ب    (8)     +d (ES) / d(t) = 0   و منه:

=   K+1 (E) (S)    (9)   k-1 (ES)  +  K+2 (ES)

اعتمادا علي نظرية المحافظة علي المادة فان:   (10)     E total = e libre  +  ES lié

e  =  Et  -  ES  (11)   

نعوض بقيمة المعدلة (11) في (9)

K+1 (S) [(Et  -  ES)] = k-1 (ES)  +  K+2 (ES)  (12) 

K+1 (S) (Et) = K+1 (S) (ES) + k-1 (ES)  +  K+2 (ES   (13) 

(ES) = K+1 (S) (Et) / K+1 (S) + ( k-1 (+  K+2 )  (14)

ادا كانت        vi = K+2 (ES)   (4)

فان Vmax = K+2 (Et)    (15)  

بقسمة المعادلة (4) علي المعادلة (15) نحصل علي المعادلة التالية:

vi /Vmax =ES/ ET .........16

      

 نعوض بقيمة المعادلة (14) في المعادلة (16)

 

            K+1 (S) (Et)

        K+1 (S) + ( k-1 +  K+2 ) Vi

                                                Vmx             (Et)                                                                            

بعد الاختصار و تبسيط المعادلة (17) نحصل علي

       (18)                           Vi   =  Vmax  × (S) 

            Km + (S) 

 وهي معادلة السرعة ل Michalis et Menten  و هي توضح العلاقة بين السرعة و الزيادة في مادة التفاعل.

بحيث    Km هو ثابت ميكائيليس  و نعبر من خلاله عن جاذبية (S)  و  (E) حيث يتناسبان  عكسيا.

و Vmax  تعبر عن السرعة القصوى للتفاعل. و عند هده السرعة تكون جميع المواقع بالإنزيم مشغولة بمادة التفاعل.

يمكن حساب المعايير الحركية للإنزيم انطلاقا من العلاقة التالية :

1-      من خلال  vi = f(s)   Michaelis et Menten (1913):  

  كما هو موضح في الشكل التالي.


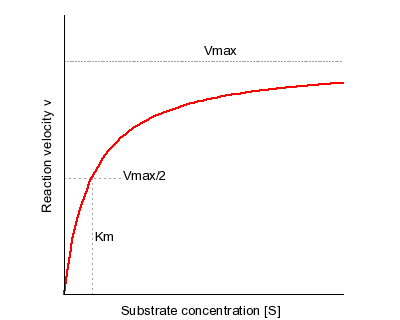
كما يمنكن حساب ثابت ميكائيليس رياضيا من العلاقة التالية: KM = K-1  + k+2  / k+1 

2-    1/vi = f (1/S)   :Linweaver et Burk(1934)



3-    Eddie et Hofstée (1952): v = f (v/S)

 

4-    Hanes (1932) : (S) / Vmax = f(S)


 

 

 

 

 

 

 

 

 

 


Cette leçon n'est pas encore prête.